最小分散デルタヘッジ法
Minimum Variance Delta Hedging
FINCAD BLOG December 13, 2016
デリバティブのポートフォリオを管理する際に、飛び抜けて重要となるギリシャ文字がデルタです。デルタは原資産の価値の微小な変化に対する、ポートフォリオの価値の感応度を示唆します。デルタは、原資産を取引することで容易に調整できます。オプショントレーダーはデルタ限度の制限を受け、通常、毎日の終わりにデルタエクスポージャーがこれらの限度内に留まっていることを保証する必要があります。限度額は原資産のドル建てポジションで表されることもあります。資産価格が$50の時にデリバティブ・ディーラーのデルタ限度額が$ 100,000であると仮定します。これはデルタを-2,000から+2,000の間に収める必要性を意味します。原資産の価値の微小な変化ΔSは、ポートフォリオ価値の 2,000ΔS未満の変化につながる必要があります。これまでデルタは、ポートフォリオの価値の原資産に対する偏微分として計算されてきました。インプライド・ボラティリティとその他の変数は一定に保たれています。現在、これは株式のための最善の方法ではない事実と、おそらく他の原資産のための最善の方法でもない可能性が認知されています。株価が変化すると、ボラティリティも変化する傾向があります。具体的には、株式の価格が上昇すると、そのボラティリティは低下する傾向があり、逆もまた真です。この現象が起きる理由に関しては2つの競合する仮説があります。1つはレバレッジが関係しています。企業の負債額はかなり静的であり、企業の資本が増加(減少)するとそのレバレッジは減少(増加)し、ボラティリティが減少(増加)する原因となります。このレバレッジ仮説では、因果関係が株価からボラティリティの方向で成立することを示唆しています。もう1つの仮説は、「ボラティリティ・フィードバック効果」として知られています。こちらの仮説では因果関係が前者と逆方向になります。ボラティリティが増加(減少)すると、株価は投資としてよりリスクが高く(低く)なり、投資家は以前より高い(低い)リターンを要求し、したがって株価は下がり(上がり)ます。
株式の価格とそのボラティリティとの間の負の相関関係を考慮するデルタの尺度を「最小分散デルタ」と呼びます。このブログでは、それを計算するための2つのアプローチを検討します。
確率的ボラティリティ・モデル
最小分散デルタを計算する1つのアプローチは、ブラックショールズ・モデルを確率論的ボラティリティ・モデルで置き換えることです。この場合、特定の株価または株価指数に依存するポートフォリオの価値を評価するためのモデルは、以下の形式をとります。
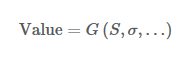
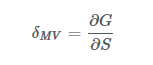
ここでδMV は、最小分散デルタを表します。しかし、この場合は確率的ボラティリティ・モデルが使用されているにもかかわらず、ボラティリティの変化なしに資産価格の変化の影響を考慮することになるため、不正確なものとなります。正しいアプローチは、
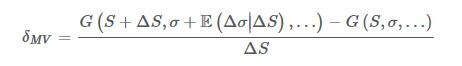
と設定することです。
ここで、Eは 期待値を表します。E(Δσ|ΔS)の項は、株価の変動の結果としての予想されるボラティリティの変化です。期待される変化の価値は、使用されている確率的ボラティリティ・モデルに依存します。例えば、資産価格のプロセスが
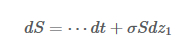
そしてこのボラティリティのプロセスが
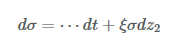
であれば
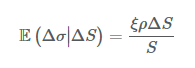
となります。
ここで、ρは 2つ の ウィーナー過程 dz1 およびdz2の間の相関です。
Bakshi et al(1997、2000)、Bartlett(2006)、Alexander and Nogueira(2007)、Alexander et al(2009)、Poulsen et al(2009)など数人の研究者がこのアプローチに従ってきました。これら共通の所見は、株価指数の場合は、確率的ボラティリティ・モデルがブラック・ショールズよりも良いデルタを生成するということです。
ベガベースモデル
オプションの値は、次のように表すことができます。
ここで、ρは 2つ の ウィーナー過程 dz1 およびdz2の間の相関です。
Bakshi et al(1997、2000)、Bartlett(2006)、Alexander and Nogueira(2007)、Alexander et al(2009)、Poulsen et al(2009)など数人の研究者がこのアプローチに従ってきました。これら共通の所見は、株価指数の場合は、確率的ボラティリティ・モデルがブラック・ショールズよりも良いデルタを生成するということです。
ベガベースモデル
オプションの値は、次のように表すことができます。
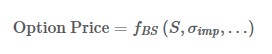
fBSはブラック・ショールズ関数であり、σimpは インプライド・ボラティリティであり、fBSの他の引数は 、大掛かりな近似をせずに定数であると仮定できる金利や配当利回りです。
この場合は以下が正しくなります。
この場合は以下が正しくなります。
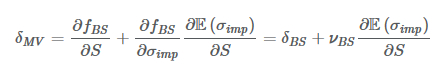
ここでδBSは、通常通り計算されるブラック・ショールズのデルタであり 、νBSはブラック-ショールズ・ベガ(インプライド・ボラティリティに関する偏微分)で、E(σimp)はSの関数としてのインプライド・ボラティリティの期待値です。偏微分について下記の仮定がなされている場合、
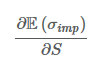
この場合は Derman および Kani (1994年)によって提案されたローカル・ボラティリティ・モデルδBS からδMVを 計算するために式(1)を使うことができ、Dupire (1994年)はこの偏微分はボラティリティ・スマイルの傾きに近いことを示唆しています(Derman et al(1995年)とColeman et al(2001年)を参照のこと)。Crépey (2004年)および Vähämaa (2004年)はこれをテストしました。Hull and White(2016年)は、異なるアプローチを試しました。彼らは経験的に偏微分を決定しようとしたのです。彼らはその偏微分がオプションの残存期間と資産価格の平方根との積で割ったδBSの2乗であるという仮定がうまく機能することを発見しました。
結論
デルタヘッジ法は簡単です。トレーダーがデルタを管理するため原資産のポジションを取る際に被る取引コストは、通常最小限に収まります。これは、オプションやその他の非線形製品のポジションが変更を行うために必要とされるベガ法やガンマヘッジ法とは対照的です。デルタヘッジ法で可能な限り大きな成果を獲得することが理にかなっています。伝統的なブラック・ショールズ・デルタから最小分散デルタへの移行でこれを行います。実際、ベガ法のリスクを軽減し、原資産の動きに関連するリスクをより正確に対処するという2つの利点があります。
参考文献
Alexander, C., A. Kaeck, and L.M. Nogueira, “Model risk adjusted hedge ratios” Journal of Futures Markets 29, 11 (2009):1021-1049.
Alexander, C. and L.M. Nogueira, “Model-free hedge ratios and scale invariant models,” Journal of Banking and Finance, 31 (2007): 1839-1861.
Bakshi, G., C. Cao, and Z. Chen, “Empirical performance of alternative option pricing models,” Journal of Finance, 52, 5 (December 1997): 2003-2049.
Bakshi, G., C. Cao, and Z. Chen, “Pricing and hedging long-term options,” Journal of Econometrics, 94 (2000): 277-318.
Bartlett, B, “Hedging Under SABR Model,” Wilmott Magazine, July / August (2006): 2-4.
Coleman, T, Y. Kim, Y. Li, and A. Verma, “Dynamic hedging with a deterministic local volatility model,” Journal of Risk, 4, 1 (2001): 63-89.
Crépey, S., “Delta-hedging vega risk,” Quantitative Finance, 4 (October 2004): 559-579.
Derman, E. and I. Kani, “Riding on a Smile,” Risk, 7 (February 1994): 32-39.
Derman, E., I. Kani, and J.Z. Zou “The Local Volatility Surface: Unlocking the Information in Index Option Prices,” Goldman Sachs Selected Quantitative Strategies Reports (December 1995).
Dupire, B. “Pricing with a smile,” Risk, 7 (February 1994):18-20.
Hull, J. and A. White, “Optimal Delta Hedging for Options,” Working Paper, University of Toronto.
Poulsen, R., K., R. Schenk-Hoppé, and C.-O Ewald, “Risk minimization in stochastic volatility models: model risk and empirical performance,” Quantitative Finance, 9, 6 (September 2009): 693-704.
Vähämaa, S., “Delta hedging with the smile,” Financial Markets and Portfolio Management, 18, 3 (2004): 241-255.
ABOUT THE AUTHOR
John Hull PhD
Professor of Finance, Co-Director of Rotman Master of Finance Program, University of Toronto, Rotman School of Management
結論
デルタヘッジ法は簡単です。トレーダーがデルタを管理するため原資産のポジションを取る際に被る取引コストは、通常最小限に収まります。これは、オプションやその他の非線形製品のポジションが変更を行うために必要とされるベガ法やガンマヘッジ法とは対照的です。デルタヘッジ法で可能な限り大きな成果を獲得することが理にかなっています。伝統的なブラック・ショールズ・デルタから最小分散デルタへの移行でこれを行います。実際、ベガ法のリスクを軽減し、原資産の動きに関連するリスクをより正確に対処するという2つの利点があります。
参考文献
Alexander, C., A. Kaeck, and L.M. Nogueira, “Model risk adjusted hedge ratios” Journal of Futures Markets 29, 11 (2009):1021-1049.
Alexander, C. and L.M. Nogueira, “Model-free hedge ratios and scale invariant models,” Journal of Banking and Finance, 31 (2007): 1839-1861.
Bakshi, G., C. Cao, and Z. Chen, “Empirical performance of alternative option pricing models,” Journal of Finance, 52, 5 (December 1997): 2003-2049.
Bakshi, G., C. Cao, and Z. Chen, “Pricing and hedging long-term options,” Journal of Econometrics, 94 (2000): 277-318.
Bartlett, B, “Hedging Under SABR Model,” Wilmott Magazine, July / August (2006): 2-4.
Coleman, T, Y. Kim, Y. Li, and A. Verma, “Dynamic hedging with a deterministic local volatility model,” Journal of Risk, 4, 1 (2001): 63-89.
Crépey, S., “Delta-hedging vega risk,” Quantitative Finance, 4 (October 2004): 559-579.
Derman, E. and I. Kani, “Riding on a Smile,” Risk, 7 (February 1994): 32-39.
Derman, E., I. Kani, and J.Z. Zou “The Local Volatility Surface: Unlocking the Information in Index Option Prices,” Goldman Sachs Selected Quantitative Strategies Reports (December 1995).
Dupire, B. “Pricing with a smile,” Risk, 7 (February 1994):18-20.
Hull, J. and A. White, “Optimal Delta Hedging for Options,” Working Paper, University of Toronto.
Poulsen, R., K., R. Schenk-Hoppé, and C.-O Ewald, “Risk minimization in stochastic volatility models: model risk and empirical performance,” Quantitative Finance, 9, 6 (September 2009): 693-704.
Vähämaa, S., “Delta hedging with the smile,” Financial Markets and Portfolio Management, 18, 3 (2004): 241-255.
ABOUT THE AUTHOR
John Hull PhD
Professor of Finance, Co-Director of Rotman Master of Finance Program, University of Toronto, Rotman School of Management
Alan White PhD
University of Toronto, Rotman School of Management
※本記事はFINCAD社の公式ブログの「MINIMUM VARIANCE DELTA HEDGING」(2016/12/13)を翻訳したものになります。
※PDF版はこちらからご覧下さい(PDF)
University of Toronto, Rotman School of Management
※本記事はFINCAD社の公式ブログの「MINIMUM VARIANCE DELTA HEDGING」(2016/12/13)を翻訳したものになります。
※PDF版はこちらからご覧下さい(PDF)
イベント・セミナー
ニュース・キャンペーン
FINCADに
関するお問い合わせ
アレクシアフィンテック株式会社
アレクシアフィンテック株式会社
03-4405-7873
- メールでのお問い合わせ
- salesdept@areccia.co.jp


